Actualizado por ultima vez el 5 de noviembre de 2021, por Luis Benites.
¿Qué es la contracción?
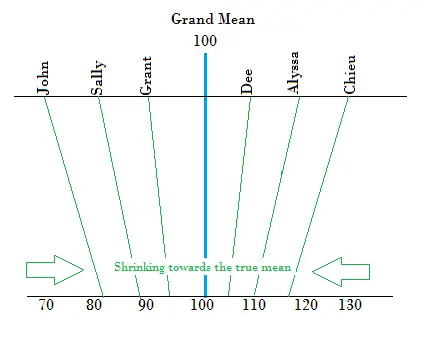
La «reducción» de las puntuaciones en un porcentaje da como resultado una mejor estimación de la media real.
La contracción es donde los valores extremos en una muestra se “encogen” hacia un valor central , como la media de la muestra . La reducción de datos puede resultar en:
- Estimaciones mejores y más estables para los parámetros reales de la población ,
- Reducción de errores de muestreo y de no muestreo ,
- Fluctuaciones espaciales suavizadas.
Sin embargo, el método tiene muchas desventajas, que incluyen:
- Errores graves si la población tiene una media atípica. Saber qué medios son “típicos” y cuáles son “atípicos” puede ser difícil ya veces imposible.
- Los estimadores reducidos pueden convertirse en estimadores sesgados , tendiendo a subestimar los verdaderos parámetros de la población.
- Los modelos ajustados reducidos pueden funcionar peor en nuevos conjuntos de datos en comparación con el conjunto de datos original utilizado para el ajuste. Específicamente, r-cuadrado «se encoge».
En el análisis bayesiano , la contracción se define en términos de priores . La contracción es donde:
“…la estimación posterior de la media anterior se desplaza de la media de la muestra hacia la media anterior” ~ Zhao et. Alabama.
Los modelos que incluyen distribuciones previas pueden resultar en una gran mejora en la precisión de un estimador reducido.
¿Qué es un estimador de contracción?
Un estimador de reducción es una nueva estimación producida al reducir una estimación sin procesar (como la media de la muestra ). Por ejemplo, se pueden combinar dos valores medios extremos para formar un valor medio más centralizado; repetir esto para todas las medias de una muestra dará como resultado una media muestral revisada que se ha “reducido” hacia la media poblacional real. Varios autores han desarrollado docenas de estimadores de contracción desde que Stein introdujo la idea por primera vez en la década de 1950. Los más populares incluyen:
- Estimador de lazo (utilizado en la regresión de lazo ),
- Estimador de cresta : se utiliza en la regresión de cresta para mejorar la estimación de mínimos cuadrados cuando hay multicolinealidad.
- Estimadores tipo Stein, incluido el estimador James-Stein “original” .
Otros métodos de contracción incluyen la regresión paso a paso , que reduce el factor de contracción a cero o uno, la regresión de ángulo mínimo y los enfoques de validación cruzada.
Referencias :
Efron B, Morris C. Análisis de datos utilizando el estimador de Stein y su generalización. Mermelada. Estadística Asoc. 1975; 70: 311–319
Horl, AE y Kennard, RW (1970). «Regresión de cresta: estimación sesgada para problemas no ortogonales». Tecnometría . vol. 12, núm. 1, págs. 55-68.
James, W. y Stein, C., (1961). «Estimación con pérdida cuadrática». Actas del Cuarto Simposio de Berkeley, vol. 1 (Berkeley, California: University of California Press), págs. 361-379.
Rolph, JE, (1976). «Elegir… estimadores para problemas de regresión». Comunicación en Estadística- Teoría y Métodos . 5(9):789-802. Enero.
Stein C. (1956). “Inadmisibilidad del estimador habitual para la media de una distribución normal multivariante ”. Actas del Tercer Simposio de Berkeley sobre Estadística Matemática y Probabilidad. vol. 1. Prensa de la Universidad de California; Berkeley, CA, EE. UU.: págs. 197–208
Zhao, Y., et. al (2010). «Sobre la aplicación del bayesiano empírico… en contextos epidemiológicos». Int J Environ Res Salud Pública. febrero de 2010; 7(2): 380–394.
Publicado en línea el 28 de enero. doi: 10.3390/ijerph7020380.

