Contenido de este artículo
- 0
- 0
- 0
- 0
Actualizado el 26 de marzo de 2022, por Luis Benites.
La navaja (“omitir uno”) se puede utilizar para reducir el sesgo y estimar los errores estándar . Es una alternativa al método bootstrap.
Comparación con Bootstrap
Al igual que el bootstrap, el Jackknife implica el remuestreo . Las principales diferencias son:
- El bootstrap involucra el muestreo con reemplazo , mientras que el jackknife involucra el muestreo sin reemplazo .
- El bootstrap tiende a ser más intensivo computacionalmente.
- El error estándar estimado de jackknife tiende a ser mayor que el remuestreo de arranque.
Descripción general del procedimiento Jackknife
La idea básica es calcular el estimador (por ejemplo , la media de la muestra ) eliminando secuencialmente una sola observación de la muestra. El estimador se vuelve a calcular hasta que haya n estimaciones para un tamaño de muestra de n . Como ejemplo simple, supongamos que tiene cinco puntos de datos X 1 , X 2 , X 3 , X 4 , X 5 . Calcularías el estimador cinco veces, para:
- X 1 , X 2 , X 3 , X 4 , X 5 .
- X 2 , X 3 , X 4 , X 5 .
- X 3 , X 4 , X 5 .
- X 4 , X 5 .
- X 5 .
Una vez que tenga sus n estimaciones
,
el error estándar se calcula con la siguiente fórmula:
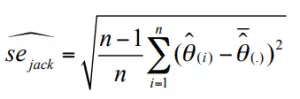
¿Por qué utilizar la estimación Jackknife?
La estimación de Jackknife generalmente se usa cuando es difícil o imposible obtener estimadores usando otro método. Por ejemplo:
- No hay base teórica disponible para la estimación,
- Es difícil trabajar con la función de estadísticas (por ejemplo, una función sin integral de forma cerrada , lo que haría que el método habitual (el método delta ) fuera imposible),
Para muestras grandes, el método Jackknife es aproximadamente equivalente al método delta.
Referencias
El cuchillo Bootstrap y Jack. Recuperado el 2 de noviembre de 2019 de: https://www.biostat.washington.edu/sites/default/files/modules/2017_sisg_1_9_v3.pdf
McIntosh, A. The Jack knife Estimation Method. Recuperado el 2 de noviembre de 2019 de: http://people.bu.edu/aimcinto/jackknife.pdf
Ramachandran, K. & Tsokos, C. (2014). Estadística Matemática con Aplicaciones en R. Elsevier .
Redactor del artículo
¿Te hemos ayudado?
Ayudanos ahora tú, dejanos un comentario de agradecimiento, nos ayuda a motivarnos y si te es viable puedes hacer una donación:La ayuda no cuesta nada
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo:
