Contenido de este artículo
- 0
- 0
- 0
- 0
Actualizado el 23 de noviembre de 2021, por Luis Benites.
El modelo GARCH , o modelo generalizado autorregresivo condicionalmente heteroscedástico , fue desarrollado por el estudiante de doctorado Tim Bollerslev en 1986. El objetivo de GARCH es proporcionar medidas de volatilidad para datos de series temporales heteoscedásticas , de la misma manera que se interpretan las desviaciones estándar en modelos más simples.
El modelo GARCH más simple es el modelo ARCH(1), que tiene muchas similitudes con los modelos AR(1). Los modelos ARCH(p) más complejos son análogos a los modelos AR(p). Finalmente, los modelos ARCH generalizados representan varianzas condicionales de la misma manera que los modelos ARMA manejan la expectativa condicional.
Usos
Los modelos GARCH tienen varias aplicaciones para el análisis de datos de series temporales en finanzas y economía. Son especialmente útiles cuando hay períodos de variación rápida (o volatilidad). Por ejemplo, pueden modelar de manera eficiente la volatilidad de los precios de los activos financieros, como bonos, índices de mercado y acciones (Francq & Zakoian, 2011).
La utilidad de un modelo GARCH no se limita a las aplicaciones financieras. Por ejemplo, Kim et al. (2014) utilizaron un modelo GARCH en su estudio comparativo de diferentes métodos de pronóstico de series temporales para predecir el volumen de pacientes en los hospitales.
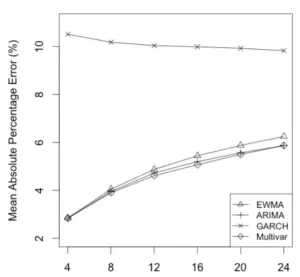
Varios métodos de pronóstico de series de tiempo comparados por Kim et al.
Heterocedasticidad y el modelo GARCH
La heterocedasticidad se refiere a las variaciones irregulares de los términos de error que se observan en un modelo de serie temporal. Las observaciones tienden a agruparse, en lugar de seguir la línea ordenada que se ve en el modelo lineal. Esto hace que el análisis de datos heteroscedásticos sea un desafío.
En su modelo convencional de mínimos cuadrados , la presencia de heteroscedasticidad puede conducir a errores estándar e intervalos de confianza demasiado estrechos , dando una falsa sensación de precisión . Los modelos GARCH abordan esto al tratar la heterocedasticidad como una varianza que se puede modelar. Luego se calculan las predicciones para la varianza de cada término de error (Engle, 2001).
Pasos básicos
Un modelo GARCH sigue tres pasos básicos:
- Estime el modelo autorregresivo de mejor ajuste.
- Calcular las autocorrelaciones del término de error,
- Prueba de significación estadística .
Estos pasos involucrados (por ejemplo, encontrar estimaciones de máxima verosimilitud del modelo condicionalmente normal) y generalmente se realizan con software. Por ejemplo, la función GARCH en R.
Referencias
Engle, R. (2001). GARCH 101: Introducción al uso de modelos ARCH/GARCH en econometría aplicada. Recuperado el 11 de mayo de 2020 de: https://www.stern.nyu.edu/rengle/GARCH101.PDF
Francq, C. & Zakoian, J. (2011). Estructura de Modelos GARCH, Inferencia Estadística y Aplicaciones Financieras . Wiley.
modelos GARCH. Recuperado el 11 de mayo de 2020 de: https://faculty.washington.edu/ezivot/econ589/ch18-garch.pdf
Kim et al. (2014). Predicción de volúmenes de pacientes en medicina hospitalaria: un estudio comparativo de diferentes métodos de pronóstico de series temporales. Recuperado el 11 de mayo de 2020 de: https://www.mcs.anl.gov/~kibaekkim/ForecastingHospitalMedicine.pdf
Redactor del artículo
¿Te hemos ayudado?
Ayudanos ahora tú, dejanos un comentario de agradecimiento, nos ayuda a motivarnos y si te es viable puedes hacer una donación:La ayuda no cuesta nada
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo:
