Contenido de este artículo
- 0
- 0
- 0
- 0
Actualizado el 10 de mayo de 2022, por Luis Benites.
En estadística, el término “intervalo de puntuación” tiene dos significados completamente diferentes. Puede referirse a:
- Intervalos de puntuación en distribuciones de frecuencia, o
- La técnica de Wilson para calcular los intervalos de confianza.
Definición 1: Intervalos de puntuación en distribuciones de frecuencia
Un intervalo de puntaje es un rango de puntajes posibles en una distribución de frecuencia o histograma [1]. Por ejemplo, el siguiente histograma de frecuencia muestra los libros y la cantidad de libros vendidos: Cada intervalo de puntaje en este histograma está representado por una barra azul: 0 a 10, 11 a 20, 21 a 30 y 31 y más.
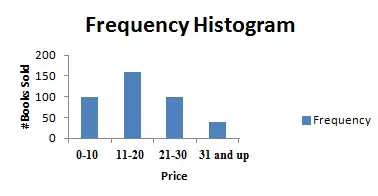
Definición 2: El intervalo de puntuación de Wilson
El intervalo de puntuación de Wilson , desarrollado por Edwin Wilson en 1927 [2], es una mejora del IC de Wald , para adaptarse a la pérdida de cobertura observada con muestras pequeñas. La idea es que utilice un valor observado para la proporción de la población , p , en lugar de una probabilidad esperada , P. La técnica también funciona bien para distribuciones asimétricas , donde p podría estar cerca de 0 o 1.
La mejora es tan marcada que se recomienda utilizar siempre el intervalo de puntuación en lugar del Wald cuando se trata de muestras pequeñas. La fórmula original de Wilson es compleja y generalmente se realiza con una computadora. Los puntos finales para un intervalo de puntuación de Wilson están dados por la fórmula a ± z (1+L) /2b, donde a y
b están dados por [3]: Sin embargo, puede obtener una buena aproximación con el siguiente procedimiento: Paso 1: Calcular y ajustada con la fórmula (y es el número de éxitos observados en la muestra): Paso 2: Calcular n ajustada con la fórmula: Paso 3: Calcular p ajustada con la fórmula: Paso 3: Sustituir p y n ajustadas de los Pasos 2 , y 3, en la fórmula del intervalo de confianza de Wald:
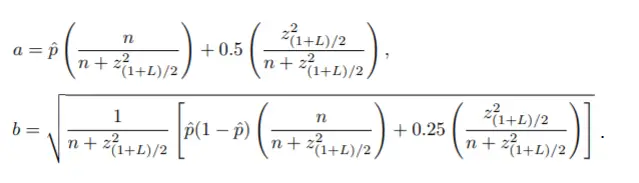
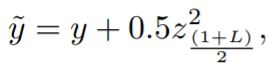
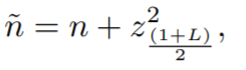
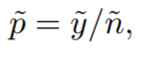
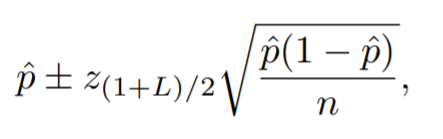Donación:
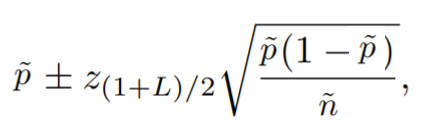
Referencias
[1] Phillips, J. (1999). Cómo pensar acerca de las estadísticas . Sexta Edición. Henry Holt y Compañía.[2] Wilson, EB 1927. Inferencia probable, ley de sucesión e inferencia estadística. Revista de la Asociación Estadounidense de Estadística 22: 209-212. PDF _
[3] Intervalos de confianza para una sola proporción poblacional. Recuperado el 6 de febrero de 2021 de: http://www.math.wpi.edu/Course_Materials/SAS/new_bici.pdf
Redactor del artículo
¿Te hemos ayudado?
Ayudanos ahora tú, dejanos un comentario de agradecimiento, nos ayuda a motivarnos y si te es viable puedes hacer una donación:La ayuda no cuesta nada
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo:
