Actualizado por ultima vez el 18 de octubre de 2022, por Luis Benites.
¿Qué es un estimador L?
Un estimador L es una combinación lineal de estadísticas basadas en estadísticas de orden o cuantiles de muestra . Los estimadores L fueron descritos por primera vez por Daniel (1920) y fueron revividos en estudios de robustez treinta años después. Tienen la ventaja de ser robustos y fáciles de usar, pero tienden a tener problemas con la baja eficiencia .
No todos los estimadores L son robustos (por ejemplo, el mínimo, el máximo y la media no se consideran robustos) y algunos tienen mejor eficiencia que otros. Las estadísticas L con ponderaciones múltiples (correctas) tenderán a ser más eficientes que aquellas con menos ponderaciones o ponderaciones mal elegidas.
Los estimadores L, T n para un tamaño de muestra n , están definidos por:
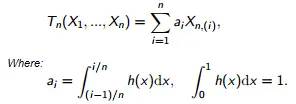
Definición formal de L-estimadores.
donde :
- X n son las estadísticas de orden,
- a i son factores de peso.
Ejemplos de estimador L
- Jurečková y Picek (2006) sugieren el rango medio como un ejemplo simple de un estimador L, que se define como:
T n = (X 1:n + X n:n ) / 2 - El rango es un estimador L simple de la escala de distribución: R n = valor más grande – valor más pequeño = X n:n – X 1:n .
- La mediana es una de las estadísticas de orden más conocidas que también es un estimador L.
- La media recortada α , que descarta los puntos de datos más pequeños y más grandes, incluye la media (α = 0), la mediana (α = 0,5).
- Media Winsorizada .
- Trimeana de Tukey .
Una clase especial de estimadores L, llamados estimadores de cuantiles kernel , utilizan un kernel (una función de densidad) como su función de peso . Varios autores han propuesto muchos otros estimadores L, incluidos Harrell y Davis (1982), quienes propusieron un nuevo estimador libre de distribución ( no paramétrico ), y Kaigh (1983), quien propuso un tipo de estadístico U no paramétrico como un cuantil . estimador.
Referencias :
Daniel, C. (1920). Observaciones ponderadas según orden. Amer. J. Matemáticas. 42, 222–236.
Harrell, FE y Davis, CE (1982), “A New Distribution-Free Quantile Estimator,” Biometrika, 69, 635-640
Jurečková,J & Picek, J. (2006). Métodos estadísticos robustos con R : Boca Raton, Fla. Chapman y Hall/CRC. ISBN 1-58488-454-1, 197 págs.
Kaigh, WD (1983), “Estimación de intervalos de cuantiles”, Communications in Statistics, Parte A: Teoría y métodos, 12, 2427-2443.
Sheather, S. y Marron, J. Kernel Quantile Estimators. Revista de la Asociación Estadounidense de Estadística
vol. 85, núm. 410 (junio de 1990), págs. 410-416

