Actualizado por ultima vez el 20 de diciembre de 2021, por Luis Benites.
¿Qué es Winsorización?
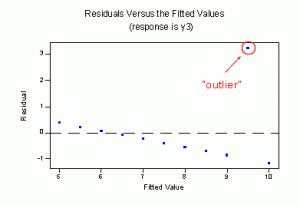
El valor atípico es claramente evidente en este gráfico residual. Imagen: PSU.edu
La winsorización es una forma de minimizar la influencia de los valores atípicos en sus datos mediante:
- Asignando al valor atípico un peso más bajo,
- Cambiar el valor para que esté cerca de otros valores en el conjunto.
Los puntos de datos se modifican , no se recortan/eliminan (como en la media recortada ).
La técnica de Winsorize fue introducida por primera vez por Dixon (1960), quien la atribuyó a Charles P. Winsor.
Estadísticas como la media y la varianza son muy susceptibles a valores atípicos; La winsorización puede ser una forma eficaz de abordar este problema, mejorar la eficiencia estadística y aumentar la solidez de las inferencias estadísticas.
La desventaja es que se introduce un sesgo en los resultados, aunque el sesgo es mucho menor que si simplemente hubiera eliminado el punto de datos. La alternativa es mantener el punto de datos tal como está, pero puede que no sea la mejor opción, ya que podría sesgar drásticamente los resultados. De cualquier manera, siempre debe tener una buena justificación para Winsorizar sus datos; Nunca ejecute el procedimiento arbitrariamente con la esperanza de obtener resultados más significativos .
Un método básico para Winsorizar a mano
- Analice sus datos para asegurarse de que el valor atípico no sea el resultado de un error de medición o algún otro error reparable.
- Decide cuánta Winsorización quieres. Esto se especifica como un porcentaje total de datos intactos . Por ejemplo, si desea Winsorizar el 5 % superior y el 5 % inferior de los puntos de datos, esto es igual a 100 % – 5 % – 5 % = 90 % Winsorización. Una Winsorización del 80 % significa que se modifica el 10 % de cada área de la cola (consulte los Consejos sobre la selección del punto de corte a continuación).
- Reemplace los valores extremos por los valores máximos y/o mínimos en el umbral. Por ejemplo:
- El siguiente conjunto de datos tiene varios extremos (en negrita):
{ 0.1, 1 , 12, 14, 16, 18, 19, 21, 24, 26, 29, 32, 33, 35, 39, 40, 41, 44, 99, 125 }
Media = 33.405. - Después de modificar el 10 % superior e inferior (comparé esos valores con el extremo más cercano):
{ 12, 12 ,12, 14, 16, 18, 19, 21, 24, 26, 29, 32, 33, 35, 39, 40, 41, 44, 44, 44 }
80 % media winsorizada = 24,95.
- El siguiente conjunto de datos tiene varios extremos (en negrita):
Puede optar por agregar un poco más a los valores más grandes/más pequeños para tener en cuenta sus pesos. por ejemplo, se modificaron los valores 99 y 125, pero 125 es aproximadamente un 125% mayor que 99. Por lo tanto, en lugar de reemplazar esos valores con 44 y 44, podría reemplazarlos con 44 y 55 (porque 125% * 44 = 55) .
¿Necesitas ayuda? ¡Consulta nuestra sección de tutorías!
Consejos sobre la selección del punto de corte
Una mala elección en el Paso 2 anterior puede dar como resultado estimadores con errores cuadráticos medios (MSE) inflados . Algunas sugerencias para elegir el punto de corte y evitar este problema:
- Compare el MSE de los resultados modificados y no modificados. Si un estimador clásico (como la media aritmética ) tiene un MSE mucho más pequeño, esto puede indicar una mala elección del punto de corte. Nota : es lógico que probablemente deba elegir el punto de corte que minimice el MSE en comparación con el estimador clásico, pero en la práctica esto es muy difícil de hacer.
- En caso de duda, consulte la literatura publicada para ver si su tipo de datos (es decir, niveles de colesterol, inteligencia, rocas minerales o algo más) es comúnmente Winsorizado y qué porcentaje se usa generalmente en su campo en particular.
- No establezca su punto de corte antes de recopilar sus datos. Espere hasta que realmente tenga los datos frente a usted antes de hacer su elección.
Referencia :
WJ Dixon (1960). Estimación simplificada a partir de muestras normales censuradas, Annals of Mathematical Statistics, 31, 385–391.
Kotz, S.; et al., editores. (2006), Enciclopedia de Ciencias Estadísticas , Wiley.
