Actualizado por ultima vez el 20 de febrero de 2022, por Luis Benites.
¿Qué son los mínimos cuadrados ponderados?
La regresión de mínimos cuadrados ponderados es una extensión de la regresión de mínimos cuadrados ordinarios. Las constantes no negativas (pesos) se adjuntan a los puntos de datos. Se utiliza cuando se cumple alguna de las siguientes condiciones:
- Sus datos violan el supuesto de homocedasticidad . En términos simples, esto significa que su variable dependiente debe agruparse con varianzas similares , creando un patrón de dispersión uniforme. Si sus datos no tienen varianzas iguales, no debe usar OLS.
- Desea concentrarse en ciertas áreas (como un valor de entrada bajo). OLS no puede «apuntar» a áreas específicas, mientras que los mínimos cuadrados ponderados funcionan bien para esta tarea. Es posible que desee resaltar áreas específicas en su estudio: aquellas que pueden ser costosas, costosas o dolorosas de reproducir. Al dar a estas áreas pesos más grandes que a otras, lleva el análisis a los datos de esa región. Esto enfoca el análisis en las áreas que importan (Shalizi, 2015).
- Está ejecutando el procedimiento como parte de una regresión logística o alguna otra función no lineal . Con cualquier procedimiento no lineal, la regresión lineal no suele ser la herramienta de modelado más adecuada a menos que pueda agrupar los datos. Además, los términos de error en la regresión logística son heteroscedásticos, lo que significa que no puede usar OLS.
- Tiene alguna otra situación en la que los puntos de datos no deben tratarse por igual. Por ejemplo, puede dar más preferencia a los puntos que sabe que se han medido con precisión y una menor preferencia a los puntos que se estiman.
Fórmula
¿ Necesita ayuda con una pregunta de tarea? ¡Mira nuestra página de tutoría!
En lugar de minimizar la suma residual de cuadrados (como se ve en OLS): minimiza la suma ponderada de cuadrados: aunque los mínimos cuadrados ponderados se tratan como una extensión de OLS, técnicamente es al revés: OLS es un caso especial de mínimo ponderado cuadrícula. Con OLS, todos los pesos son iguales a 1. Por lo tanto, resolver la fórmula WSS es similar a resolver la fórmula OLS. Sin embargo, es poco probable que realmente resuelva esto a mano, ya que la mayoría de los paquetes de software de estadísticas decentes los tendrán integrados.
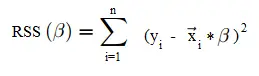
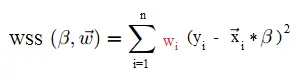
Ventajas y desventajas
Los mínimos cuadrados ponderados tienen varias ventajas sobre otros métodos, que incluyen:
- Es muy adecuado para extraer la máxima información de pequeños conjuntos de datos.
- Es el único método que se puede utilizar para puntos de datos de calidad variable.
Las desventajas incluyen:
- Requiere que sepa exactamente cuáles son los pesos. La estimación de pesos puede tener resultados impredecibles, especialmente cuando se trata de muestras pequeñas. Por lo tanto, la técnica solo debe usarse cuando sus estimaciones de peso son bastante precisas. En la práctica, la precisión de las estimaciones de peso no suele ser posible.
- La sensibilidad a los valores atípicos es un problema. Un valor atípico deshonesto que recibe una ponderación inapropiada podría sesgar drásticamente sus resultados.
Alternativas
WLS solo se puede usar en los casos excepcionales en los que sabe cuáles son las estimaciones de peso para cada punto de datos. Cuando la heterocedasticidad es un problema, es mucho más común ejecutar OLS en su lugar, utilizando un estimador de varianza de diferencia . Por ejemplo, White (1980) sugiere reemplazar S 2 (X’X) -1 por X’DX. Este es un estimador consistente para X’ΩX: mientras que el estimador consistente de White no requiere heterocedasticidad, no es una estrategia muy eficiente. Sin embargo, si no conoce los pesos de sus datos, puede ser su mejor opción. Si desea una explicación completa de cómo implementar el estimador consistente de White, puede leer el artículo original de White de 1908 de forma gratuita aquí .
Referencias :
Agresti A. (1990) Análisis de datos categóricos. John Wiley and Sons, Nueva York.
Kotz, S.; et al., editores. (2006), Enciclopedia de Ciencias Estadísticas , Wiley.
Estadísticas de Ingeniería. Manual. Consultado el 20 de febrero de 2018 en: http://www.itl.nist.gov/div898/handbook/pmd/section1/pmd143.htm
Shalizi, C. (20150. Lecture 24–25: Weighted and Generalized Least Squares. Consultado en febrero 20, 2018 de: http://www.stat.cmu.edu/~cshalizi/mreg/15/lectures/24/lecture-24–25.pdf
White, Halbert (1980) “A Heteroscedasticity-Consistent Covariance Matrix Estimator y una prueba directa de heteroscedasticidad». Econometrica . 48 (4): 817–838. doi: 10.2307/1912934
