Contenido de este artículo
Actualizado el 18 de octubre de 2022, por Luis Benites.
¿Qué es un estimador consistente?
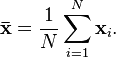
La media muestral es un estimador consistente de la media poblacional.
Una estimación consistente tiene errores insignificantes (variaciones) a medida que aumenta el tamaño de las muestras . Más específicamente, la probabilidad de que esos errores varíen en más de una cantidad determinada se aproxima a cero a medida que aumenta el tamaño de la muestra. En otras palabras, cuantos más datos recopile, un estimador consistente estará cerca del parámetro de población real que está tratando de medir. La media muestral y la varianza muestral son dos estimadores consistentes bien conocidos.
La idea de coherencia también se puede aplicar a la selección de modelos , en la que se selecciona de forma coherente el modelo «verdadero» con los parámetros «verdaderos» asociados. Por ejemplo, una prueba de bondad de ajuste también se puede utilizar como medida de consistencia. Una prueba popular de bondad de ajuste es la prueba de chi-cuadrado , que funciona bajo la premisa de que los valores esperados para sus datos se ajustan a una distribución normal . Y si tiene datos de un modelo de serie temporal , la consistencia de los datos se puede medir con un modelo autorregresivo . Existen muchas otras medidas de consistencia para ajustar los datos a los modelos. El método que utilice depende de lo que desee que midan sus datos. Por ejemplo, ¿piensa que sus datos siguen una tendencia lineal , una tendencia exponencial o una tendencia específica como la que se ve en este documento , que describe un estimador consistente para los componentes de perturbación en los modelos financieros?
Orígenes
El término estimador consistente es la abreviatura de » secuencia consistente de estimadores», una idea que se encuentra en la convergencia en probabilidad . La idea básica es que repite los resultados del estimador una y otra vez, con tamaños de muestra en constante aumento. Eventualmente, suponiendo que su estimador sea consistente, la secuencia convergerá en el verdadero parámetro de población . Esta convergencia se denomina límite , que es un componente fundamental del cálculo .
Referencias :
Cramér, H. (1946). Métodos matemáticos de estadística”, Princeton Univ. Prensa IA Ibragimov, RZ [RZ Khas’minskii] Has’minskii, (1981) “Estimación estadística: teoría asintótica”, Springer. (Traducido del ruso)
Levinsohn, J. & MacKie-Mason, J. (1989). Un simple, contras. est. para componentes de perturbaciones en modelos financieros. Oficina Nacional de Investigación Económica. Documento de trabajo técnico n.º 80. Consultado el 7 de enero de 2017 en http://www.nber.org/papers/t0080.pdf.
¿Te hemos ayudado?
Ayudanos ahora tú, dejanos un comentario de agradecimiento, nos ayuda a motivarnos y si te es viable puedes hacer una donación:La ayuda no cuesta nada
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo:
