Distancia de Mahalanobis: definición simple, ejemplos

Actualizado el 21 de julio de 2024, por Luis Benites.

¿Cuál es la distancia de Mahalanobis?

La distancia de Mahalanobis (MD) es la distancia entre dos puntos en un espacio multivariado . En un espacio euclidiano regular , las variables (por ejemplo, x, y, z) se representan mediante ejes trazados en ángulo recto entre sí; La distancia entre dos puntos cualesquiera se puede medir con una regla. Para variables no correlacionadas, la distancia euclidiana es igual a la MD. Sin embargo, si dos o más variables están correlacionadas , los ejes ya no están en ángulo recto y las mediciones se vuelven imposibles con una regla. Además, si tiene más de tres variables, no puede trazarlas en un espacio 3D regular. El MD resuelve este problema de medición, ya que mide distancias entre puntos, incluso puntos correlacionados para múltiples variables.

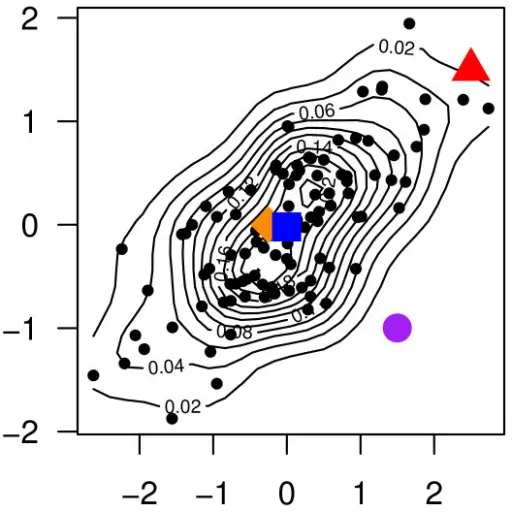
Ejemplo de diagrama de distancia de Mahalanobis. Un gráfico de contorno superpuesto al gráfico de dispersión de 100 extracciones aleatorias de una distribución normal bivariada con media cero, varianza unitaria y correlación del 50 % . El centroide definido por las medias marginales se indica con un cuadrado azul.

La distancia de Mahalanobis mide la distancia relativa al centroide, una base o punto central que se puede considerar como una media general para datos multivariados. El centroide es un punto en el espacio multivariante donde se cruzan todas las medias de todas las variables. Cuanto mayor sea el MD, más alejado del centroide estará el punto de datos.

Usos

El uso más común de la distancia de Mahalanobis es encontrar valores atípicos multivariados , lo que indica combinaciones inusuales de dos o más variables. Por ejemplo, es bastante común encontrar una mujer de 6 pies de altura que pese 185 libras, pero es raro encontrar una mujer de 4 pies de altura que pese tanto.

Definicion formal

La distancia de Mahalanobis entre dos objetos se define (Varmuza & Filzmoser, 2016, p.46) como:
d (Mahalanobis) = [(x _B – x _A ) ^T * C ^-1 * (x _B – x _A )] ^0.5
Donde :
x _A y x _B es un par de objetos, y
C es la matriz de covarianza de la muestra .

Otra versión de la fórmula, que utiliza las distancias de cada observación a la media central:
d i = [x _i – x̄) ^t C ^-1 (x _i – x̄)] ^0.5
Donde:
x _i = un vector de objeto
x̄ = vector de media aritmética

Medidas relacionadas

Un término relacionado es apalancamiento , que utiliza una escala de medición diferente a la distancia de Mahalanobis. Los dos están relacionados por la siguiente fórmula (Weiner et. al, 2003): Distancia de
Mahalanobis = ( N – 1) (H _ii – 1/ N )
Donde h _ii es el apalancamiento.

Mientras que el MD solo usa variables independientes en sus cálculos, la distancia de Cook usa tanto las variables independientes como las dependientes . Es producto del apalancamiento y del residual estudentizado .

Desventajas

Aunque la distancia de Mahalanobis se incluye con muchos paquetes estadísticos populares, algunos autores cuestionan la confiabilidad de los resultados (Egan & Morgan, 1998; Hadi & Simonoff, 1993).

Un problema importante con el MD es que se necesita el inverso de la matriz de correlación para los cálculos. Esto no se puede calcular si las variables están altamente correlacionadas (Varmuza & Filzmoser, 2016).

Referencias

Egan, W. y Morgan, S. (1998). Detección de valores atípicos en datos químicos analíticos multivariados. Química Analítica, 70, 2372-2379.
Hadi, A. y Simonoff, J. (1993). Procedimientos para la identificación de múltiples valores atípicos en modelos lineales. Revista de la Asociación Estadounidense de Estadística, 88, 1264-1272.
Hill, T. et. Alabama. (2006). Estadísticas: métodos y aplicaciones: una referencia completa para la ciencia, la industria y la minería de datos. Statsoft, Inc.
Varmuza, K. & Filzmoser, P. Introducción al análisis estadístico multivariado en quimiometría. CRC Press
Weiner, I. et. Alabama. (2003). Manual de Psicología, Métodos de Investigación en Psicología . John Wiley & Sons.