Contenido de este artículo
Actualizado el 29 de septiembre de 2021, por Luis Benites.
¿Qué es la ortogonalidad en estadística?
En pocas palabras, ortogonalidad significa «no correlacionado». Un modelo ortogonal significa que todas las variables independientes en ese modelo no están correlacionadas. Si una o más variables independientes están correlacionadas , entonces ese modelo no es ortogonal .
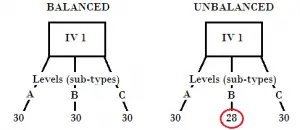
El diseño de la izquierda está equilibrado porque tiene niveles uniformes.
El término «ortogonal» generalmente solo se aplica al ANOVA clásico . Un ANOVA ortogonal tiene todas las variables categóricas independientes y cada celda en una tabla de doble entrada tiene el mismo número de observaciones (llamado diseño balanceado ). Por otro lado, los modelos lineales generales nunca son ortogonales, ya que al menos una variable independiente no es categórica (los GLM tienen una variable continua ).
En las estadísticas basadas en el cálculo , también puede encontrarse con funciones ortogonales , definidas como dos funciones con un producto interno de cero. Son particularmente útiles para encontrar soluciones a ecuaciones diferenciales parciales como la ecuación de Schrödinger y las ecuaciones de Maxwell.
Ejecución de pruebas con ortogonalidad
La ortogonalidad también hace una diferencia en cómo se ejecutan las pruebas estadísticas. Los modelos ortogonales solo tienen una forma de estimar los parámetros del modelo y ejecutar pruebas estadísticas. Los modelos no ortogonales tienen varias formas de hacer esto, lo que significa que los resultados pueden ser más complicados de interpretar. En general, una mayor correlación entre las variables independientes significa que debe interpretar el resultado con más cautela.
Si un modelo es ortogonal o no ortogonal es a veces una decisión de juicio. Por ejemplo, supongamos que tiene cuatro celdas en un ANOVA: tres celdas tienen 10 sujetos y la cuarta celda tiene 9 sujetos. Técnicamente, este es un diseño no balanceado (y por lo tanto no ortogonal). Sin embargo, el tema que falta en una celda tendrá muy poco impacto en los resultados. En otras palabras, puede tratar este diseño semidesequilibrado como ortogonal.
Raíces en álgebra matricial
El término ortogonalidad proviene del álgebra matricial . Dos vectores son ortogonales si la suma de los productos de los elementos cruzados es cero. Por ejemplo, los productos cruzados de estos dos vectores son cero: 2(4) + 3(-4) + 4(1) + 0(2) = 0. (Ver: multiplicación de matrices para saber por qué esto funciona). El mismo concepto ( es decir, la multiplicación de matrices) se puede aplicar a las celdas en una tabla de doble entrada. La ortogonalidad está presente en un modelo si los efectos de cualquier factor suman cero en los efectos de cualquier otro factor en la tabla.
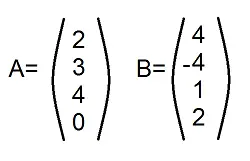
Referencias
Cañada, S. (2020). Funciones ortogonales.
