Actualizado por ultima vez el 18 de agosto de 2021, por Luis Benites.
¿Qué es Mega Millions?
Mega Millions es un juego de lotería en el que eliges seis números de dos grupos de números:
- Cinco números entre 1 y 70 (“bolas blancas”)
- Un número del 1 al 25 («megabola de oro»)
En enero de 2021, el premio mayor alcanzó los mil millones de dólares.
Una valla publicitaria para los premios de los juegos de lotería Powerball y Mega Millions en Missouri.
¿Cuáles son las probabilidades de Mega Millions?
Según el sitio web oficial de Mega Millions, las probabilidades de ganar el premio mayor en Mega Millions son de 1 en 302,6 millones, lo que CNBC [1] llama probabilidades «asombrosas». Tienes quinientas veces más probabilidades de morir al caerte de una escalera en el próximo año (1 en 583,019)[2] que ganar ese premio mayor con un solo boleto.
Probabilidades y premios de Mega Millions
Tus probabilidades generales de ganar un premio son de 1 en 24, pero no te emociones demasiado: el premio con las mejores probabilidades (1 en 37) es de solo dos dólares. Aquí hay un resumen de las probabilidades:
- Solo Mega Ball ($2): 37 a 1
- 1 número más la Mega Ball ($4): 89 a 1
- 2 números más la Mega Ball ($10): 693 a 1
- 2 números ($10): 606 a 1
- 3 números más el Mega Ball ($200): 14,547 a 1
En este punto, las probabilidades comienzan a aumentar. Para poner esto en perspectiva, es mucho más probable que un inodoro te lastime de forma no fatal (1 en 5000) [3] que elegir los 3 números correctos más la bola Mega.
- 4 números ($500): 38,792 a 1
- 4 números más el Mega Ball ($10,000): 931,001 a 1
- 5 números ($1 millón): 12,607,306 a 1
Aquí es donde las probabilidades están tan en tu contra que puede ser difícil visualizarlas. Imagina que estás en el estadio más grande del mundo que está lleno hasta su capacidad de 150.000. Ahora imagina que hay una rifa para un auto. Sus probabilidades de ganar: 1 en 500.000. Para igualar las probabilidades de ganar el premio mayor de Mega Millions, debe tener 605 estadios, uno al lado del otro.
¿Cómo se calculan las probabilidades de Mega Millions?
El cálculo de posibilidades involucra varios elementos:
- Cuántos números tienes para elegir (70).
- Cuántos números eliges. Para Mega Millions, son 5 (más una Mega Ball, que veremos en el siguiente paso).
- Cuántos números no eliges. 70 – 5 = 65.
El número de coincidencias correctas entre su elección y los números que extrae la máquina de lotería (¡Con suerte, los 5!).
Reemplazando esos números en la fórmula de combinaciones , obtenemos:
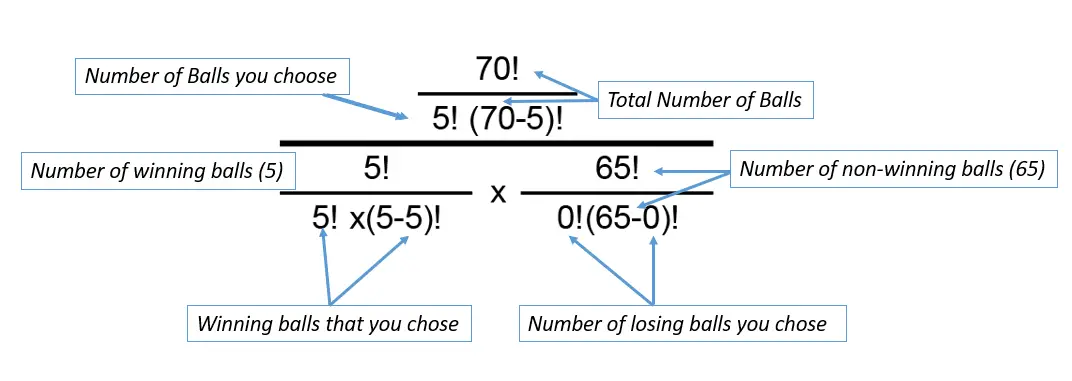
Si calculas esto en una calculadora, obtienes 12,103,104. Estos son los pasos (El ! es un factorial ). Finalmente, tenemos que multiplicar esto por las combinaciones de números de Mega Balls. Hay 25 bolas, y solo eliges una, entonces: 12,103,014 * 25 = 302,575,350.
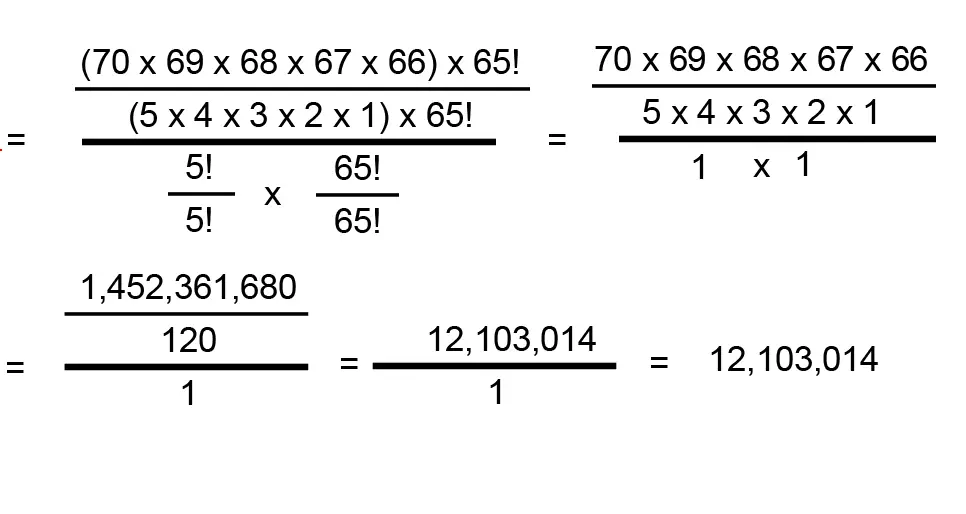
Como solo elige una de estas combinaciones posibles, sus probabilidades son de 302,575,349 a 1.
¿Puedo mejorar mis probabilidades de Mega Millions?
Como todos los juegos de lotería, puede mejorar sus probabilidades un poco (es decir, no mucho) al:
- Comprar más de un boleto para el mismo juego. Puede aumentar sus ganancias en Mega Millions gastando $ 1 adicional en un «Megaplier», pero esto no aumenta sus probabilidades.
- Evite los números de la suerte tradicionales: 7, 11, 13. Evite elegir los números del 1 al 31, que son los cumpleaños, lo que significa que muchas personas elegirán estos números de la «suerte». Excepción: elija los números 21 y 23; Como se indicó en el artículo anterior sobre las probabilidades de lotería , estas bolas tienen más tinta, por lo que es más probable que sean elegidas.
Referencias
Cartelera de Powerball: Tony Webster de Minneapolis, Minnesota, Estados Unidos, CC BY 2.0 a través de Wikimedia Commons
[1] CNBC: https://www.cnbc.com/2021/01/21/how-to-up-the-odds- of-wining-a-lottery-harvard-professor.html
[2] III Hechos, Estadísticas, Riesgos de Mortalidad .
[3] CDC: https://www.cdc.gov/mmwr/preview/mmwrhtml/mm6022a1.htm?s_cid=mm6022a1_w
