Actualizado por ultima vez el 5 de febrero de 2022, por Luis Benites.
La prueba de Brunner Munzel (también llamada prueba de Wilcoxon generalizada ) es una prueba estadística no paramétrica para la igualdad estocástica de dos muestras . La igualdad estocástica es una medida de similitud entre dos poblaciones , lo que significa que las poblaciones tienen aproximadamente la misma frecuencia de valores mayores.
La prueba de BM no está ampliamente disponible en software estadístico. Hay algunas macros R y SAS, pero tienden a dar resultados inconsistentes (LaBone et al., 2013).
Cuándo usar la prueba de Brunner Munzel
Esta prueba robusta de heteroscedasticidad se puede utilizar como una alternativa a la prueba de suma de rangos de Wilcoxon-Mann-Whitney (WMW) (Fagerland, 2012). La prueba BM permite empates y ajustes para varianzas desiguales , por lo que, a diferencia de la prueba de Mann Whitney, no requiere la suposición de varianzas iguales entre dos grupos.
la prueba BM funciona bien para valores empatados, datos categóricos ordenados y puede usarse tanto para distribuciones continuas como discretas (LaBone, 2013). Es una prueba aproximadamente válida de una hipótesis nula débil para muestras suficientemente grandes (Lin, 2013).
Como la mayoría de las pruebas no paramétricas, la prueba de Brunner Munzel es más adecuada para muestras pequeñas. La prueba requiere al menos diez observaciones por grupo para aplicar la aproximación de muestra pequeña con la distribución t y funciona bien para tamaños de muestra de 30 o más (Neuhauser, 2011). Si el tamaño de la muestra es inferior a 10, la prueba de BM permutada es una mejor opción.
Estadística de prueba de BM
La hipótesis nula para la prueba es H 0 = 0.5, lo que implica igualdad estocástica. La hipótesis alternativa es H 0 ≠ 0.5, lo que significa que en uno de los grupos se dan valores mayores. Si se rechaza la hipótesis nula, debe interpretarse vagamente en el sentido de que las poblaciones difieren de alguna manera.
El estadístico de prueba de Brunner Munzel se calcula con la fórmula (LaBone, 2013) Donde:
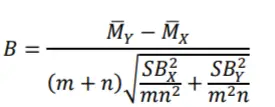
- M x y M y son las medias de los rangos medios para las muestras X e Y,
- m, n son el número de observaciones en las dos muestras,
- SB son las estimaciones de varianza para X e Y.
Brunner y Munzel sugieren usar una distribución t con una aproximación de Welch-Satterthwaite para los grados de libertad .
Referencias
Brunner, E. y Munzel, U. (2000), «El problema no paramétrico de Behrens-Fisher: teoría asintótica y una aproximación de muestra pequeña», Biometrical Journal, 42, 17-25
Fagerland, M. (2012). Pruebas t, pruebas no paramétricas y grandes estudios: ¿una paradoja de la práctica estadística? d Metodología de investigación médica de BMC 2012, 12:78
http://www.biomedcentral.com/1471-2288/12/78
LaBone et al. (2013). Respuesta a los comentarios de SC&A sobre ORAUT-RPRT-0053. Recuperado el 25 de enero de 2021 de: https://www.cdc.gov/niosh/ocas/pdfs/dps/dc-orrprt53-r0.pdf
Lin, W. (2013). Ensayos sobre inferencia causal en experimentos aleatorios. Recuperado el 25 de enero de 2021 de: https://www.stat.yale.edu/~wl389/winston-thesis.pdf
Neuhauser, M. (2011). Pruebas estadísticas no paramétricas Un enfoque computacional. Prensa CRC.

