Actualizado por ultima vez el 12 de marzo de 2022, por Luis Benites.
¿Qué es una región de rechazo?
Una región de rechazo es un área de un gráfico donde rechazaría la hipótesis nula (suponiendo que los resultados de su prueba se encuentren dentro de esa área). Mire el video para obtener una descripción general:
¿Qué es una región de rechazo? 
Mira este video en YouTube .
¿No puedes ver el vídeo? Haga clic aquí
El propósito principal de la estadística es probar teorías o resultados de experimentos. Por ejemplo, es posible que hayas inventado un nuevo fertilizante que crees que hace que las plantas crezcan un 50 % más rápido. Para probar que su teoría es verdadera, su experimento debe:
- Sea repetible.
- Compararse con un hecho conocido sobre las plantas (en este ejemplo, probablemente la tasa de crecimiento promedio de las plantas sin fertilizante).
Llamamos a este tipo de prueba estadística una prueba de hipótesis . La región de rechazo (también llamada región crítica) es parte del proceso de prueba. Específicamente, es un área de probabilidad que le dice si su teoría (su “”hipótesis”) es probablemente cierta.
Regiones de rechazo y distribuciones de probabilidad
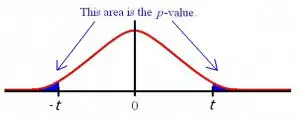
Las regiones de rechazo en una distribución t de dos colas. Imagen: ETSU.edu
Cada región de rechazo se puede dibujar en una distribución de probabilidad . La imagen de arriba muestra una distribución t con una región de dos colas. También es posible tener una región de rechazo solo en una cola.
Dos colas contra una cola
Qué tipo de prueba está determinada por su declaración de hipótesis nula . Por ejemplo, si su declaración pregunta «¿Es la tasa de crecimiento promedio mayor a 10 cm por día?» esa es una prueba de una cola, porque solo está interesado en una dirección (más de 10 cm por día). También podría tener una sola región de rechazo para «menos de». Por ejemplo, «¿La tasa de crecimiento es inferior a 10 cm por día?» Se usaría una prueba de dos colas , con dos regiones, cuando desee saber si hay una diferencia en ambas direcciones (mayor que y menor que).
Regiones de rechazo y niveles alfa
Usted, como investigador, elige el nivel alfa que está dispuesto a aceptar. Por ejemplo, si quisiera tener un 95 % de confianza en que sus resultados son significativos , elegiría un nivel alfa del 5 % (100 % – 95 %). Ese nivel del 5% es la región de rechazo . Para una prueba de una cola, el 5% estaría en una cola. Para una prueba de dos colas, la región de rechazo estaría en dos colas.
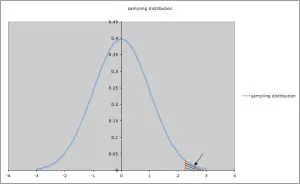
Una prueba de una cola con la región de rechazo en una cola.
Regiones de rechazo y valores P.
Hay dos formas de probar una hipótesis: con un valor p y con un valor crítico .
Método del valor p : cuando ejecuta una prueba de hipótesis (por ejemplo, una prueba z ), el resultado de esa prueba será un valor p . El valor p es un “valor de probabilidad”. Es lo que te dice si tu declaración de hipótesis es probablemente verdadera o no. Si el valor cae en la región de rechazo, significa que tiene resultados estadísticamente significativos ; Puede rechazar la hipótesis nula . Si el valor p cae fuera de la región de rechazo, significa que sus resultados no son suficientes para descartar la hipótesis nula. ¿Qué es estadísticamente significativo ? En el ejemplo del fertilizante para plantas, un resultado estadísticamente significativo sería uno que mostrara que el fertilizante hace que las plantas crezcan más rápido (en comparación con otros fertilizantes).
Método de la Región de Rechazo con un valor crítico : Los pasos son exactamente los mismos. Sin embargo, en lugar de calcular un valor p, calcula un valor crítico. Si el valor cae dentro de la región, rechaza la hipótesis nula.
Siguiente : ¿Qué es una región de aceptación?
¡ Visite nuestro canal de YouTube para obtener más ayuda y consejos sobre estadísticas!
Referencias
Beyer, WH CRC Standard Mathematical Tables, 31ª ed. Boca Raton, FL: CRC Press, págs. 536 y 571, 2002.
Dodge, Y. (2008). La Enciclopedia Concisa de Estadística . Saltador.
Lindström, D. (2010). Schaum’s Easy Outline of Statistics , segunda edición (Schaum’s Easy Outlines) 2ª edición. Educación McGraw-Hill
Wheelan, C. (2014). Estadísticas desnudas . WW Norton y compañía
