Contenido de este artículo
Actualizado el 23 de enero de 2022, por Luis Benites.
El coeficiente de incertidumbre, también llamado coeficiente de entropía o competencia, es una medida de la entropía (es decir, incertidumbre ) en una variable de columna Y que explica una variable de fila X. A veces se expresa en símbolos como o U(X|Y) o U(C|R), donde C son columnas y R son filas.
Nota de desambiguación : Theil (1970) derivó una gran parte del coeficiente de incertidumbre, por lo que ocasionalmente se lo denomina «U de Theil». Esto es un poco engañoso, porque el término U de Theil generalmente se refiere a una U completamente diferente: las estadísticas U que se usan en finanzas. Ver : U: Estadística / Theil’s U.
Cálculo del coeficiente de incertidumbre
Los coeficientes de incertidumbre oscilan entre 0 y 1, ambos inclusive. Podemos calcularlo con la fórmula:
U(X|Y)= 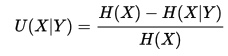 .
.
H(X) es la entropía de una sola distribución. La entropía puede ser cualquier número de 0 a ln(A), donde A es el número de puntos de datos. Una entropía baja significa una correlación muy fuerte ; una alta entropía implica baja correlación y por lo tanto baja incertidumbre. La entropía H(X) se puede calcular mediante
![]()
La entropía relativa de X dado Y, H(X|Y), se calcula mediante
![]() El símbolo sigma (Σ) es una notación de suma y significa «sumar».
El símbolo sigma (Σ) es una notación de suma y significa «sumar».
El coeficiente de incertidumbre simétrico
El coeficiente de incertidumbre analizado es una medida de comparación y no es simétrico. El coeficiente de incertidumbre simétrico U (también escrito a veces U(X, Y)) es lo que obtenemos cuando tomamos el promedio ponderado de U(X|Y) y U(Y|X). Esto se calcularía por:
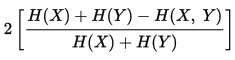
Puntos Fuertes del Coeficiente de Incertidumbre
El coeficiente de incertidumbre se usa principalmente para verificar qué tan efectivo o válido es un algoritmo estadístico en particular. Dado que verifica la correlación, no la «corrección», no penalizará un modelo algorítmico solo porque predice la clase incorrecta. En cambio, penaliza la inconsistencia. Esto significa que no se ve afectado por las fracciones (relativas) de las diferentes clases que se configuran.
Esto lo distingue de otras formas en las que puede probar la precisión, formas como la precisión (es decir , el valor predicho positivo ) y la recuperación (la tasa positiva verdadera o la sensibilidad de una prueba ). El coeficiente de incertidumbre es particularmente útil cuando se evalúan algoritmos de agrupamiento . (Estos no tienen un orden particular, y la evaluación ciega del orden del coeficiente nos permite llegar al corazón de la correlación).
Referencias
Nehmzów, U. (2006). Métodos científicos en robótica móvil: análisis cuantitativo del comportamiento de los agentes. Ciencia Springer.
Instituto SAS (1999). Medidas de Asociación. Recuperado de http://www.okstate.edu/sas/v8/sashtml/stat/chap28/sect20.htm el 30 de diciembre de 2017
Theil, H. (1970). Sobre la estimación de relaciones que involucran variables cualitativas. Revista americana de sociología. vol. 76, No. 1 (julio), págs. 103-154
Vogt, WP (2005). Diccionario de estadística y metodología: una guía no técnica para las ciencias sociales . SABIO.
¿Te hemos ayudado?
Ayudanos ahora tú, dejanos un comentario de agradecimiento, nos ayuda a motivarnos y si te es viable puedes hacer una donación:La ayuda no cuesta nada
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo:
