Contenido de este artículo
Actualizado el 8 de enero de 2022, por Luis Benites.
La distribución gamma es una familia de distribuciones de probabilidad continuas sesgadas a la derecha . Estas distribuciones son útiles en la vida real donde algo tiene un mínimo natural de 0. Por ejemplo, se usa comúnmente en finanzas, para tiempos transcurridos o durante procesos de Poisson .
PDF de distribución gamma
Si X es una variable aleatoria continua entonces la función de distribución de probabilidad es: Donde
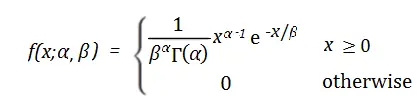
- Γ(x) = la función gamma ,
 .
. - α = El parámetro de forma .
- β (a veces se usa θ en su lugar) = El parámetro de tasa (el recíproco del parámetro de escala ).
α y β son mayores que 1.
Cuando α = 1, se convierte en la distribución exponencial .
Cuando β = 1, se convierte en la distribución gamma estándar .
Alfa y beta definen la forma del gráfico. Aunque ambos tienen un efecto en la forma, un cambio en β mostrará un cambio brusco, como lo muestran las líneas rosas y azules en este gráfico:
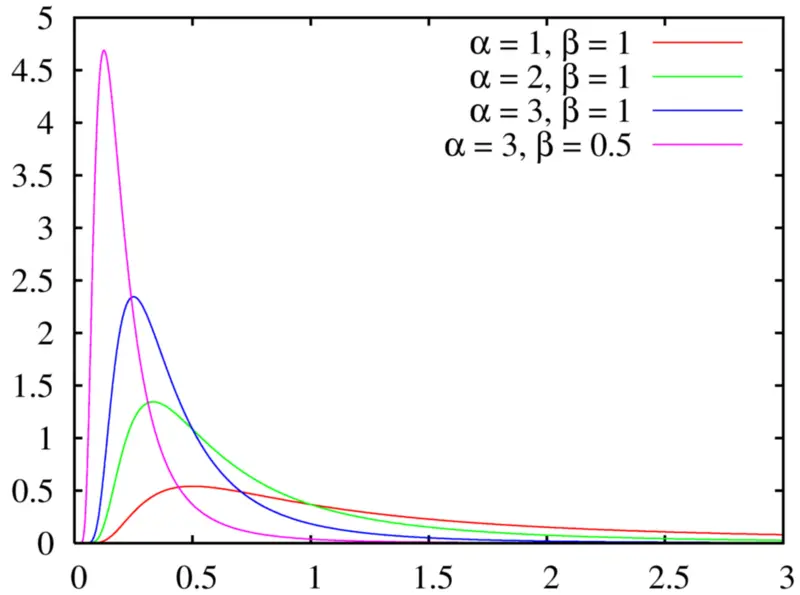
El efecto de cambiar alfa y beta en la forma de la distribución gamma.
Puede pensar en α como el número de eventos que está esperando (aunque α puede ser cualquier número positivo, no solo números enteros ), y β como el tiempo medio de espera hasta el primer evento. Si α (número de eventos) permanece sin cambios pero β (tiempo medio entre eventos) aumenta, tiene sentido que el gráfico se desplace hacia la derecha ya que los tiempos de espera se alargarán. De manera similar, si el tiempo medio de espera (β) permanece igual pero el número de eventos (α) aumenta, la gráfica también se desplazará hacia la derecha. A medida que α se acerca al infinito, la gamma se acerca mucho a la distribución normal .
Media, Varianza, MGF
Media : E(X) = αβ
Varianza : var(X) = αβ 2
Función generadora de momentos : MX (t) = 1 /(1 − βt) α
(Artemiou, 2009)
Cómo encontrar probabilidades de distribución gamma en Excel
Paso 1: Escriba «=GAMMA.DIST(» en una celda vacía.
Paso 2: Escriba el valor donde desea encontrar la probabilidad. Por ejemplo, si desea encontrar la probabilidad en x=6, la función se convierte en «= DISTR.GAMMA( 6”
Paso 3: Escriba sus valores α y β, separados por una coma. Por ejemplo, si su α es 3 y β es 2, la función se convierte en: “=DIST.GAMMA( 6, 3, 2”
Paso 4: escriba FALSO, cierre los paréntesis y luego presione la tecla «enter». La función completa es «=GAMMA.DIST(6, 3, 2, FALSE» Excel devolverá la probabilidad como 0.112020904.
Sugerencia : para encontrar la probabilidad acumulada, escriba VERDADERO en lugar de FALSO en el Paso 4.
MATLAB.
La distribución gamma se calcula en MATLAB utilizando el objeto prob.GammaDistribution. Puede encontrar instrucciones completas sobre cómo encontrar la distribución en MATLAB aquí en el sitio de MathWorks .
Distribuciones relacionadas
La gamma es un caso especial de la distribución Tweedie (cuando p = 2).
Para grados de libertad enteros , la distribución de Wishart es la contraparte multivariante de la distribución gamma.
La distribución gamma inversa tiene la misma distribución que el recíproco de una distribución gamma. Se utiliza principalmente en las pruebas de hipótesis bayesianas .
La distribución Erlang y la distribución chi-cuadrado son casos especiales de la distribución gamma. La distribución de Erlang ocurre cuando α es cualquier número entero positivo. La distribución exponencial también es un caso especial de la distribución gamma. La gamma y la exponencial son muy similares, como lo muestra este gráfico. Las dos curvas tienen medias idénticas pero diferentes desviaciones estándar :
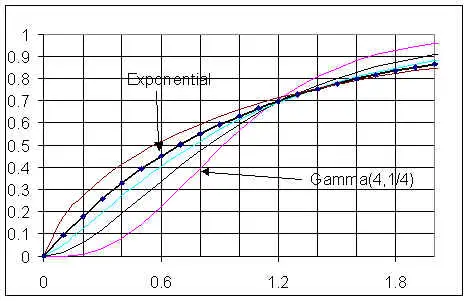
El Gaussiano Inverso también tiene una forma similar a la gamma. De hecho, pueden verse exactamente iguales con los parámetros correctos. Sin embargo, es más fácil producir valores extremadamente grandes con la Gaussiana inversa.
Referencias
Artemiou, A. (2009). Capítulo 4 — Clase 4 La Distribución Gamma y sus Relativos. Recuperado el 3 de noviembre de 2017 de: http://www.math.mtu.edu/~aartemio/Courses/Stat318/Lectures/Chapter4/Chapter4_Lecture4.pdf.
Beyer, WH CRC Standard Mathematical Tables, 28.ª ed. Boca Ratón, Florida: CRC Press, pág. 534, 1987.
Papoulis, A. Probabilidad, variables aleatorias y procesos estocásticos, 2ª ed. Nueva York: McGraw-Hill, págs. 103-104, 1984.
¿Te hemos ayudado?
Ayudanos ahora tú, dejanos un comentario de agradecimiento, nos ayuda a motivarnos y si te es viable puedes hacer una donación:La ayuda no cuesta nada
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo:
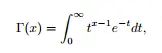 .
. 