Contenido de este artículo
Actualizado el 22 de mayo de 2022, por Luis Benites.
Una distribución límite (también llamada distribución asintótica ) es la distribución hipotética, o convergencia , de una secuencia de distribuciones. Como es hipotético, no es una distribución en el sentido general de la palabra. La teoría de la distribución asintótica intenta encontrar una distribución límite a una serie de distribuciones.
Algunas de estas distribuciones son bien conocidas. Por ejemplo, la distribución muestral del estadístico t convergerá a una distribución normal estándar si el tamaño de la muestra es lo suficientemente grande. A veces, la distribución de probabilidad límite se puede encontrar estudiando el comportamiento de CDF o PDF . Los teoremas como el de Slutsky también se pueden usar para explorar la convergencia en las distribuciones de probabilidad.
¿Por qué necesitamos encontrar distribuciones hipotéticas?
En estadística básica , el proceso consiste en tomar una muestra aleatoria de observaciones y ajustar esos datos a una distribución conocida como la distribución normal o la distribución t . Cuando ajusta datos a un modelo, no es una ciencia exacta. Ajustar los datos exactamente a una distribución conocida suele ser muy difícil en la vida real debido a los tamaños de muestra limitados, lo que da como resultado una «mejor suposición» basada en lo que sabe (o lo que sabe su software) sobre el comportamiento de las estadísticas de muestras grandes. La distribución limitante/asintótica se puede utilizar en muestras pequeñas y finitas para aproximar la verdadera distribución de una variable aleatoria, una que encontraría si el tamaño de la muestra fuera lo suficientemente grande.
Limitar las distribuciones de probabilidad es importante cuando se trata de encontrar tamaños de muestra apropiados . Cuando el tamaño de una muestra es lo suficientemente grande, la distribución de una estadística formará una distribución límite (suponiendo que exista tal distribución).
Limitación de la distribución y el CLT
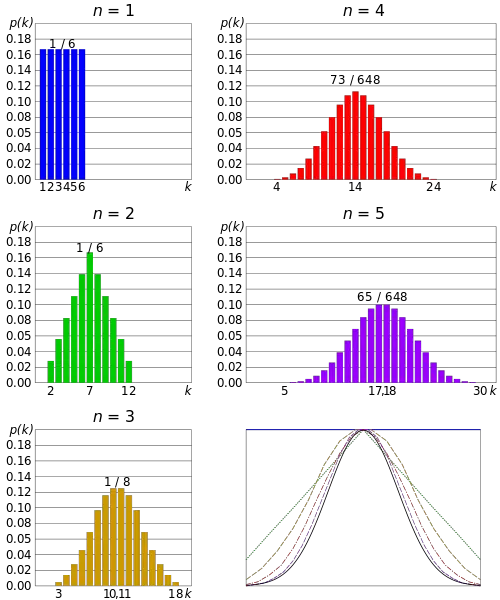
Una serie de lanzamientos de dados converge a una distribución normal a medida que aumenta el tamaño de la muestra. Crédito de la foto:cmglee|Wikimedia Commons
El Teorema del Límite Central (CLT) utiliza el concepto de límite para describir el comportamiento de las medias muestrales .
El CLT nos dice que la distribución muestral de las medias muestrales se aproxima a una distribución normal a medida que aumenta el tamaño de la muestra, sin importar la forma de la distribución de la población. Lo que esto significa es que, si toma más muestras (especialmente las más grandes), el gráfico de las medias de la muestra se parecerá cada vez más a una distribución normal, incluso si su gráfico está sesgado o no es normal . En otras palabras, la distribución límite para un gran conjunto de medias muestrales es la distribución normal.
Definicion formal
Epps (2013) le da al término un marco más formal:
Supongamos que X n es una secuencia aleatoria con cdf F n (X n y X es una variable aleatoria con cdf F(x).
Si F n converge a F cuando n > ∞ (para todos los puntos donde F(x) es continua), entonces la distribución de x n converge a x. Esta distribución se llama la distribución límite de x n .
En términos más simples, podemos decir que la distribución de probabilidad límite de Xn es la distribución límite de alguna función de Xn .
Distribución Limitada y Cadenas de Markov
Una de las áreas más comunes donde aparece el término es en el estudio de las Cadenas de Markov . Cuando el tiempo n > ∞, una cadena de Markov tiene una distribución límite π = (π j ) j∈s . Se puede encontrar un valor para π resolviendo una serie de ecuaciones lineales .
Referencias:
Epps, T. (2013). Probabilidad y Teoría Estadística para Investigadores Aplicados . Científico Mundial.
Abramowitz, M. y Stegun, IA (Eds.). Manual de funciones matemáticas con fórmulas, gráficos y tablas matemáticas, novena edición. Nueva York: Dover, 1972.
Feller, W. “The Fundamental Limit Theorems in Probability”. Toro. Amer. Matemáticas. Soc. 51, 800-832, 1945.
Kallenberg, O. Fundamentos de la probabilidad moderna . Nueva York: Springer-Verlag, 1997.
Spiegel, MR Teoría y Problemas de Probabilidad y Estadística . Nueva York: McGraw-Hill, págs. 112-113, 1992.
¿Te hemos ayudado?
Ayudanos ahora tú, dejanos un comentario de agradecimiento, nos ayuda a motivarnos y si te es viable puedes hacer una donación:La ayuda no cuesta nada
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo:
