Distribución de cola pesada y distribución de cola ligera: definición y ejemplos

Actualizado el 22 de mayo de 2022, por Luis Benites.

¿Qué es una distribución de cola pesada?

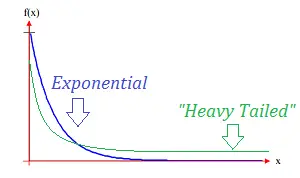Una distribución de cola pesada tiene una cola más pesada que una distribución exponencial (Bryson, 1974). En otras palabras, una distribución con colas pesadas llega a cero más lentamente que una con colas exponenciales; habrá más volumen bajo la curva del PDF . Las distribuciones de colas pesadas tienden a tener muchos valores atípicos con valores muy altos. Cuanto más pesada sea la cola, mayor será la probabilidad de que obtenga uno o más valores desproporcionados en una muestra .

Características de la Distribución de Cola Pesada

Si toma una muestra aleatoria de la distribución, es probable que termine con una muestra formada principalmente por valores pequeños. Pero probablemente habrá uno o más valores muy grandes que desequilibrarán sus estadísticas . Por ejemplo, si toma una muestra de los ingresos de las personas en los Estados Unidos, la mayor parte de sus datos será relativamente pequeña, alrededor de $ 50,000. Sin embargo, uno o dos valores en su muestra podrían ser ridículamente grandes (es decir, valores atípicos). Podría dibujar 99 artículos que cuestan alrededor de $ 50,000, luego un «Bill Gates»: gana varios miles de millones de dólares por año.

Estos valores grandes tienden a sesgar las estadísticas de la muestra: la media sería muy engañosa (para el ejemplo anterior, estaría en millones de dólares), la varianza de la muestra probablemente será muy grande y la media de la muestra suele subestimar la media de la población . Otro par de peculiaridades con colas pesadas:

1. El teorema del límite central no funciona.
2. Algunos momentos no existen, por lo que en su lugar se utilizan estadísticas de pedidos .

Distribuciones de cola pesada en el mundo real

Muchas situaciones del mundo real son complicadas, incluyendo:

• El 0,1% superior de la población de EE. UU. posee tanto como el 90% inferior ( Guardián ).
• Los tamaños de archivo en las computadoras tienden a ser pequeños, con algunos archivos muy grandes incluidos ( Columbia ).
• Los tamaños de las páginas web y las cargas de trabajo de los sistemas informáticos tienden a ser pesados ​​( Stanford ).
• Los pagos de seguros y las devoluciones financieras siguen un patrón similar ( Wolfram ).

Ejemplos de distribución de cola pesada

Muchas distribuciones son de cola pesada, incluyendo:

• Distribución Cauchy
• Distribución Frechet
• Distribución LogNormal
• Distribución de Pareto
• Distribución t de Student
• Distribución Zipf

Distribución de Cauchy.

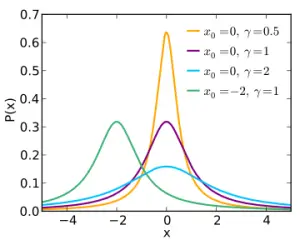
La distribución de Cauchy. La curva morada es la distribución estándar de Cauchy. Imagen: Skbkekas | Wikimedia Commons.

El Cauchy es similar a una distribución normal , excepto que tiene colas más pesadas y un pico más alto. Es ampliamente conocido por el hecho de que su valor esperado no existe.
Log distribución normal .

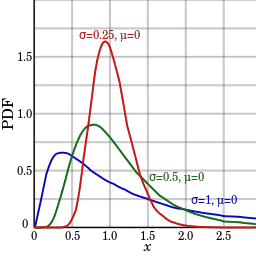
Algunos ejemplos de funciones de densidad lognormales. Imagen: Por Krishnavedala|Wikimedia Commons

Una distribución lognormal (log-normal o Galton) es una distribución de probabilidad con un logaritmo distribuido normalmente .

Subclases de cola pesada

Distribución de cola gruesa: una distribución de cola pesada con varianza infinita . Tenga en cuenta que algunos autores usan el término «cola gorda» y «cola pesada» indistintamente, especialmente en finanzas y comercio.

Regularmente variable : el comportamiento de las colas se desvía de las leyes puras de potencia (Mikosch, 1999).

Subexponencial : Una distribución donde el valor más grande en una muestra hace una contribución muy grande a la suma total (Mikosch, 1999).

Distribución de cola larga : una distribución de cola pesada con una cola larga. Algunos autores usan el término cola larga como sinónimo de «cola ligera» (ver definición más abajo), aunque el consenso general es que una cola larga es un subconjunto de cola pesada. Para aumentar la confusión, otros hacen una distinción entre una cola delgada (en comparación con la exponencial) y una cola con una apariencia larga, como en una cola muy, muy, muy larga (imagínese 50 desviaciones estándar de la media, y usted Empezaré a sacar la distinción). La clave aquí es leer la intención del autor con mucho cuidado, ya que están usando el término «cola larga».

¿Qué es una distribución de cola ligera?

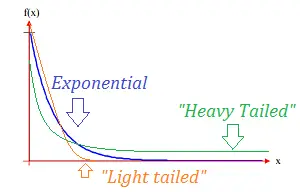
Las distribuciones de probabilidad que tienen colas más delgadas que una distribución exponencial son distribuciones de cola ligera. Llegan a cero mucho más rápido que las exponenciales, por lo que tienen menos masa en la cola. La distribución de Gumbel es un ejemplo de una distribución de cola ligera. La mayoría de las distribuciones que le presentan en las estadísticas elementales (por ejemplo, la distribución normal y la distribución t ) son en realidad de cola ligera; Estos no reflejan muy bien los datos del “mundo real” Nair et. al, 2013).

Referencias

Bryson, M. (1974). Distribuciones de cola pesada: propiedades y pruebas. Technometrics 16(1):61-68 (febrero de 1974).
Mikosch, T. (1999). Variación Regular, Subexponencialidad y sus Aplicaciones en la Teoría de la Probabilidad.
Recuperado el 10 de diciembre de 2017 de: https://www.eurandom.tue.nl/reports/1999/013-report.pdf
Nair, J. et al., (2013). Los fundamentos de colas pesadas (PPT). Recuperado el 7 de diciembre de 2017 de: http://users.cms.caltech.edu/~adamw/papers/2013-SIGMETRICS-heavytails.pdf