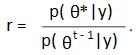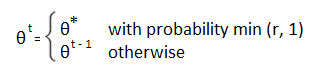Contenido de este artículo
Actualizado el 1 de enero de 2022, por Luis Benites.
El algoritmo Metropolis-Hastings es uno de los muchos algoritmos de muestreo que pertenecen a la clase general de algoritmos Markov Chain Monte Carlo . Uno de los tipos más simples de algoritmos MCMC, recibió su nombre de Metropolis et al. (1953) y Hastings (1970).
El algoritmo se utiliza en las pruebas de hipótesis bayesianas para muestrear distribuciones posteriores , donde el muestreo directo es difícil o imposible. Puede aproximarse a una distribución posterior (es decir, crear un histograma ) compuesta por cualquier combinación de probabilidades previas y modelos de muestreo . También se puede utilizar para la integración de Monte Carlo para calcular los valores esperados . Al igual que otros métodos MCMC, generalmente se usa para problemas multidimensionales , en teoría también se puede usar para problemas unidimensionales . Sin embargo, existen métodos más sencillos para problemas unidimensionales, como el muestreo por rechazo adaptativo.
El algoritmo de metrópolis
El algoritmo Metropolis es una adaptación de caminata aleatoria combinada con un muestreo de aceptación-rechazo que converge en una distribución objetivo específica (Gelman et al., 2013).
Los pasos básicos para el algoritmo Metropolis (de Gelman et. al) son:
- Elija un punto inicial θ 0 de una distribución inicial, donde p(θ 0 |y) > 0. Esta puede ser una estimación muy aproximada.
- Para todos los valores de t 1,2,…, Muestree una propuesta θ * de una “distribución de propuesta”, que debe ser una distribución simétrica . θ * se muestrea en el momento t, J t ( θ * | θ t-1 )
- Calcular la relación de densidad:

- Colocar:

Una explicación simple de los pasos
Los pasos anteriores pueden ser un poco difíciles de comprender si es nuevo en estadísticas bayesianas y distribuciones anteriores . Sin embargo, puede tener una buena idea de lo que implica imaginarse que está de vacaciones en Orlando. Su objetivo es visitar tantas atracciones turísticas importantes como sea posible, maximizando su tiempo en las principales atracciones y minimizando su tiempo en lugares impopulares. Desde tu punto de partida (digamos que es un parque temático que crees que podría ser popular), debes decidir si vas a:
- Quédese en su ubicación actual,
- Muévase a la atracción occidental más cercana, o
- Vaya a la atracción del este más cercana.
Desafortunadamente, perdiste tu guía y tu teléfono celular. Así que no tienes idea de qué atracciones son las más populares, ni sabes cuántas atracciones hay. Dicho esto, tiene un punto de partida, por lo que puede preguntar en la oficina del parque temático cuántos visitantes reciben cada día. Como no sabes adónde ir después, lanzas una moneda. Cara, ve al oeste. Tails, ve hacia el este. Para este ejemplo, volteas cruz. Salta a la siguiente atracción hacia el este en un tiempo récord y pregunta en la oficina qué tan popular es la atracción. Si la nueva atracción (también conocida como la distribución de la propuesta) es más popular, te quedas allí. Si es menos popular, calculará la probabilidad de mudarse según la popularidad de su ubicación actual (p actual ) y la popularidad de su ubicación propuesta (p propuesto ), que es:
p mover = (p propuesto ) / (p actual )
Creas una ruleta circular tosca con un plato de papel y pajita de un restaurante de comida rápida, marcando valores de cero a 1 en la parte exterior del plato. Giras el plato y anotas el número del borde del plato. Si el valor está entre cero y p move , te mueves. Cualquier otra cosa, te quedas.
Lo anterior parece simplista, pero funciona: la probabilidad de que estés en cualquier atracción coincide con el número relativo de visitantes de esa atracción. (Adaptado de Kruschke, 2010).
Algoritmo Metropolis vs Algoritmo Metropolis-Hastings
El algoritmo Metropolis es un caso especial del algoritmo general Metropolis-Hastings (Hoff, 2009). La principal diferencia es que el algoritmo Metropolis-Hastings no tiene el requisito de distribución simétrica (en el paso 2 anterior). Si usa una distribución simétrica, se debe hacer un ajuste a R (Paso 4) (Gelman, 2013): El algoritmo Metropolis puede ser lento, especialmente si su punto de partida inicial está muy lejos del objetivo. El uso de distribuciones de propuestas asimétricas (es decir, el uso del Algoritmo Metropolis-Hastings más general) puede acelerar el proceso.
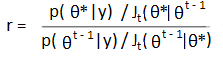
Referencias
Gelman, A. et al. (2013). Análisis de datos bayesianos, tercera edición. Prensa CRC.
Hastings, W. (1970). «Métodos de muestreo de Monte Carlo utilizando cadenas de Markov y su aplicación».
Biometrika, 57: 97–109.
Hoff, P. (2009). Un primer curso en métodos estadísticos bayesianos . Medios de comunicación de ciencia y negocios de Springer.
Kruschke, J. (2010). Realización de análisis de datos bayesianos: una introducción al tutorial con R. Academic Press.
Metrópolis, N.; Rosenbluth, AW; Rosenbluth, MN; Cajero, AH; Teller, E. (1953). “Ecuaciones de Cálculos de Estado por Máquinas de Computación Rápida”. Revista de Física Química. 21 (6): 1087–1092.
¿Te hemos ayudado?
Ayudanos ahora tú, dejanos un comentario de agradecimiento, nos ayuda a motivarnos y si te es viable puedes hacer una donación:La ayuda no cuesta nada
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo: