Actualizado por ultima vez el 11 de febrero de 2022, por Luis Benites.
En un sentido general, infinitamente divisible significa que cualquier sección de tiempo y espacio se puede dividir en un número infinito de piezas cada vez más pequeñas. Por ejemplo, 10 pies se pueden subdividir en secciones de 1 pie, secciones de 0,1 pies, secciones de 0,00001 pies… y así sucesivamente. Sin embargo, la divisibilidad infinita en la teoría de la probabilidad tiene un significado más definido. Específicamente:
Una distribución de probabilidad es infinitamente divisible si se puede escribir como la suma de n variables aleatorias independientes e idénticamente distribuidas para cualquier número entero positivo n.
La divisibilidad infinita es una propiedad importante de las distribuciones de probabilidad estables . A menudo se ven en usos prácticos, como la teoría del tiempo de espera y los problemas de modelado, así como en aplicaciones teóricas como los teoremas de límites .
Definición de divisibilidad infinita
Si la distribución de probabilidad F es infinitamente divisible, entonces para cualquier entero positivo n, existe una variable S n que se puede escribir como
S norte = X norte 1 + X norte 2 + …. + X norte norte
tales que cada una de las X n son variables aleatorias, independientes e idénticamente distribuidas; su suma, S n , tiene la distribución de probabilidad F.
Divisibilidad infinita y funciones características
Una de las formas más fáciles de averiguar si una función es infinitamente divisible es mirar su función característica . Eso es porque, si Φ(ω) es una función característica de su distribución F y Φ n (ω) es la función característica de cada una de sus variables distribuidas idénticamente independientes, entonces:
Φ(ω) = [Φ norte (ω)] norte .
(Recuerde, todos tienen distribuciones de probabilidad idénticas, por lo que su función característica es la misma).
Entonces, podemos derivar la función característica de nuestras variables aleatorias sumadas de nuestra función de probabilidad original mirando el inverso de eso,
Φ norte (ω) = [Φ(ω)] 1/ n .
Esta útil fórmula nos permite probar si una distribución de probabilidad es o no infinitamente divisible. Nuestro primer paso puede ser calcular la función característica hipotética de los sumandos, si es que existen.
Ejemplos de distribuciones de probabilidad infinitamente divisibles
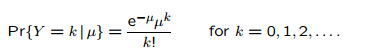
PMF para la distribución de Poisson.
La distribución de Poisson es una distribución infinitamente divisible.
Para cada μ >0, y cada n∈ {1, 2, 3,…}, las variables aleatorias independientes X n 1 , X n 2 ,…X n n tienen una distribución de Poisson.
La distribución normal , la distribución chi-cuadrado y la distribución de Cauchy también son ejemplos de distribuciones infinitamente divisibles. De hecho, toda distribución estable es infinitamente divisible. Sin embargo, lo contrario no es cierto: no todas las distribuciones infinitamente divisibles son estables.
La distribución binomial y la distribución uniforme no son infinitamente divisibles; lo mismo es cierto para cualquier distribución que esté acotada, restringida a un cierto rango (Sato, 1999).
Referencias
Sato, Ken-iti (1999). Procesos de Lévy y distribuciones infinitamente divisibles. Prensa de la Universidad de Cambridge. pag. 31.
Sheffield, S. (2014) Divisibilidad infinita y procesos de Lévy. Artículo publicado en el sitio web MIT.edu. Recuperado el 24 de noviembre de 2017 de: https://ocw.mit.edu/courses/mathematics/18-175-theory-of-probability-spring-2014/lecture-slides/MIT18_175S14_Lecture20.pdf
Watkins, T. (nd) Infinitely Variables aleatorias divisibles y sus funciones características, artículo publicado en el sitio web de la Universidad de San José. Recuperado el 24 de noviembre de 2017 de: http://www.sjsu.edu/faculty/watkins/infdiv.htm
