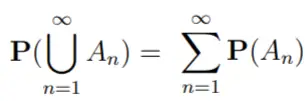Contenido de este artículo
Actualizado el 13 de diciembre de 2021, por Luis Benites.
Una medida de probabilidad da probabilidades a un conjunto de resultados experimentales (eventos). Es una función sobre una colección de eventos que asigna una probabilidad de 0 y 1 a cada evento, cumpliendo ciertas condiciones.
El papel de una medida de probabilidad es cuantificar la probabilidad de cada resultado de cada evento en el álgebra σ (una colección de conjuntos que tienen ciertas propiedades); En pocas palabras, el σ-álgebra asigna una probabilidad a un evento (p. ej., “lloverá hoy”) y al complemento de ese evento (p. ej., “hoy no lloverá”) y la unión (“lloverá hoy, o no lloverá hoy”). t”) [2].
Ejemplos de medidas de probabilidad
Para una tirada de un dado de seis caras , el espacio muestral (Ω) = {1, 2, 3, 4, 5, 6}. Si A = {1, 3, 5} es el evento de que la tirada es impar, entonces P (A) = ½.
Ejemplo continuo uniforme : supongamos que desea elegir un número aleatorio entre 0 y 1, donde todos los números son igualmente probables. El espacio muestral es el intervalo cerrado [0, 1]; La probabilidad para cualquier intervalo dentro de [0, 1] es la longitud de I. En términos generales, la medida de probabilidad uniforme en [a, b] se puede definir como [3]:
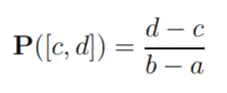
Definición formal de medida de probabilidad
Una medida de probabilidad P sobre F es una función de valor real P sobre F con tres propiedades [2]:
- P (A) ≥ 0, para A ∈ F
- PAG (Ω) = 1, PAG (∅) = 0,
- Para la secuencia disjunta de eventos (es decir, A i ∩ A j = ∅ para i ≠ j) entonces:

- ∅ = el conjunto vacío ,
- ∩ = intersección ,
- ∪ = unión ,
- A c = complemento (el conjunto de resultados en Ω que no están en A),
- ∈ = es un elemento de (está en el conjunto),
- F = una colección de subconjuntos de Ω
- σ-campo = Una colección de subconjuntos de Ω es un σ-campo si:
- Ω ∈ F
- UN ∈ F → UN C ∈ F
- UN norte ∈ F para norte = 1, 2, 3, … ∪ ( n = 1→∞) UN norte ∈ F
Donde:
Referencias
[1] Probabilidad . Recuperado el 11 de marzo de 2021 de: https://cims.nyu.edu/~cfgranda/pages/DSGA1002_fall15/material/probability_1.pdf[2] Kennedy, T. Medida de probabilidad y variables aleatorias. Recuperado el 11 de marzo de 2021 de: https://www.math.arizona.edu/~tgk/mc/prob_background.pdf
[3] Probabilidades. Recuperado el 11 de marzo de 2021 de: https://www.math.arizona.edu/~tgk/464_10/chap1_8_26.pdf
¿Te hemos ayudado?
Ayudanos ahora tú, dejanos un comentario de agradecimiento, nos ayuda a motivarnos y si te es viable puedes hacer una donación:La ayuda no cuesta nada
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo: