Parametrización: ¿Qué significa parametrizar?

Actualizado el 29 de octubre de 2021, por Luis Benites.

Este artículo trata sobre la definición de distribuciones de probabilidad usando parámetros . Si está tratando de averiguar sobre parámetros de población (cubiertos en estadísticas elementales ), consulte: ¿Qué es un parámetro en estadística?

¿Qué es la Parametrización?

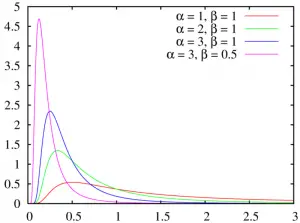
La familia de distribución gamma , que muestra algunas de las posibles opciones de parámetros.

En pocas palabras, la parametrización (o parametrización) es donde cambia ciertos aspectos de una distribución de probabilidad ajustando sus parámetros.

Se pueden usar muchos parámetros diferentes para definir una distribución de probabilidad. Por ejemplo:

• Las distribuciones normales se parametrizan por su media (un parámetro de ubicación ) y su desviación estándar (un parámetro de escala ).
• La distribución beta tiene dos parámetros de forma positivos que controlan la forma de la distribución.
• La distribución gamma tiene un parámetro de forma y un parámetro de velocidad.

Más específicamente, cuando parametriza, especifica una curva o forma con valores en un rango específico . Las familias paramétricas tienen muchos parámetros posibles; lo que elija es generalmente una cuestión de conveniencia, simplicidad y utilidad (Breiman, 1973).

Una definición más formal

Se puede utilizar una función para representar la parametrización. De hecho, la función que define un modelo estadístico a veces se denomina parametrización del modelo. La función se toma de un conjunto θ con valores en P tal que θ → P ^θ (Commenges, 2004). La notación es la siguiente:

• P = familia de probabilidades,
• Π = (P ^θ ; θ ∈ Θ)—Una parametrización para una determinada familia de probabilidades. Las parametrizaciones de la misma familia de probabilidades se pueden denotar con Π ₁ , Π ₂ … Π _n .

Sin embargo, una función no es suficiente por sí sola para definir un modelo. Un modelo identificable es uno con parámetros conocidos y un conjunto de variables aleatorias .

Parametrización frecuentista frente a bayesiana

En las estadísticas frecuentistas , la parametrización no cambia las probabilidades en el modelo. Simplemente cambia la ubicación en la recta numérica, la forma general o la extensión. Sin embargo, en la teoría bayesiana, puede dar lugar a nuevos antecedentes y nuevos modelos (Gelman, 2004).

Referencias

Breiman, L. (1973). Estadística: con miras a las aplicaciones. Houghton Mifflin.
Cominges, D. (2009). Modelos estadísticos: Verosimilitud convencional, penalizada y jerárquica. Encuestas Estadísticas. vol. 3 (2009) 1–17.
Gelman, A. (2004). Parametrización y Modelado Bayesiano . Revista de la Asociación Estadounidense de Estadística. Volumen 99, 2004 – Número 466.

`