Actualizado por ultima vez el 20 de enero de 2022, por Luis Benites.
¿Qué es la dispersión?
La dispersión en estadística es una forma de describir qué tan disperso está un conjunto de datos. Cuando un conjunto de datos tiene un valor grande, los valores del conjunto están muy dispersos; cuando es pequeño, los elementos del conjunto están muy agrupados. Muy básicamente, este conjunto de datos tiene un valor pequeño:
1, 2, 2, 3, 3, 4
…y este conjunto tiene uno más amplio:
0, 1, 20, 30, 40, 100
La dispersión de un conjunto de datos se puede describir mediante un rango de estadísticas descriptivas que incluyen la varianza , la desviación estándar y el rango intercuartílico . La dispersión también se puede mostrar en gráficos: diagramas de puntos , diagramas de caja y diagramas de tallo y hoja tienen una mayor distancia con muestras que tienen una mayor dispersión y viceversa.
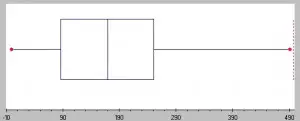
Cuanto más grande sea la caja, mayor será la dispersión en un conjunto de datos. Imagen: Universidad de Seton Hall
Medidas de dispersión.
- Coeficiente de dispersión : Un término general para una variedad de fórmulas, incluida la distancia entre cuartiles .
- Desviación estándar : probablemente la medida más común. Te dice qué tan separados están los números de la media,
- Índice de Dispersión : una medida de dispersión comúnmente utilizada con variables nominales .
- Rango intercuartil (IQR) : describe dónde se encuentra la mayor parte de los datos (el » cincuenta medio «).
- Rango interdecil : la diferencia entre el primer decil (10%) y el último decil (90%).
- rango : la diferencia entre el número más pequeño y el más grande en un conjunto de datos.
- Diferencia de medias o diferencia de medias: mide la diferencia absoluta entre el valor medio en dos grupos diferentes en ensayos clínicos.
- Desviación absoluta mediana (MAD) : la mediana de las desviaciones absolutas de la mediana de un conjunto de datos.
- Cuartiles : Números que dividen los datos en cuatro cuartos (cuartiles primero, segundo, tercero y cuarto).
En algunos procesos, como la fabricación o la medición, la baja dispersión se asocia con una alta precisión. La alta dispersión se asocia con una baja precisión.
Medidas de Dispersión: Ejemplo
Digamos que se le pidió que comparara las medidas de dispersión de dos conjuntos de datos. El conjunto de datos A tiene los elementos 97,98,99,100,101,102,103 y el conjunto de datos B tiene los elementos 70,80,90,100,110,120,130. Al observar los conjuntos de datos, probablemente pueda decir que las medias y las medianas son las mismas (100), lo que técnicamente se denomina «medidas de tendencia central» en estadística. Sin embargo, el rango (que le da una idea de qué tan disperso está todo el conjunto de datos) es mucho mayor para el conjunto de datos B (60) en comparación con el conjunto de datos A (6). De hecho, casi todas las medidas de dispersión serían diez veces mayores para el conjunto de datos B, lo cual tiene sentido ya que el rango es diez veces mayor. Por ejemplo, observe las desviaciones estándar de los dos conjuntos de datos: Desviación estándar para A: 2.160246899469287.
Desviación estándar para B: 21,602468994692867.
La cifra del conjunto de datos B es exactamente diez veces la de A.
Advertencia : cuando use una calculadora (o una fórmula), verifique que esté usando la configuración (o fórmula) correcta para sus datos. Muchas medidas de dispersión (como la varianza) tienen dos fórmulas diferentes, una para una población y otra para una muestra. Si no está seguro si tiene una muestra o una población, lea estos artículos:
¿Qué es una población en estadística?
Muestra en estadística: Qué es, cómo encontrarlo .
Echa un vistazo a nuestro canal de YouTube de estadísticas . Cientos de videos básicos para una variedad de temas de estadísticas elementales .
Referencias
Beyer, WH CRC Standard Mathematical Tables, 31ª ed. Boca Raton, FL: CRC Press, págs. 536 y 571, 2002.
Kotz, S.; et al., editores. (2006), Enciclopedia de Ciencias Estadísticas , Wiley.
Levine, D. (2014). Incluso usted puede aprender estadísticas y análisis: una guía fácil de entender sobre estadísticas y análisis, 3.ª edición. Pearson FT Press
Salkind, N. (2016). Estadísticas para personas que (creen que) odian las estadísticas: uso de Microsoft Excel 4.ª edición.
