Modelo de ecuaciones simultáneas (SEM): definición simple

Actualizado el 21 de julio de 2024, por Luis Benites.

Es posible que desee leer este otro artículo primero: ¿Qué es la simultaneidad?

¿Qué es un modelo de ecuaciones simultáneas (SEM)?

Un modelo de ecuaciones simultáneas (SEM) es un modelo en forma de un conjunto de ecuaciones lineales simultáneas . Cuando el análisis de regresión introductorio introduce modelos con una sola ecuación (por ejemplo , regresión lineal simple ), los modelos SEM tienen dos o más ecuaciones. En un modelo de ecuación única, los cambios en la variable de respuesta (Y) ocurren debido a cambios en la variable explicativa (X); en un modelo SEM, otras variables Y se encuentran entre las variables explicativas en cada ecuación SEM. El sistema está determinado conjuntamente por las ecuaciones del sistema; En otras palabras, el sistema exhibe algún tipo de simultaneidad o causalidad de “ida y vuelta” entre las variables X e Y.

Ejemplo SEM

El mercado de enfermeras graduadas está influenciado por:

• comportamiento de la demanda,
• comportamiento de la oferta,
• Niveles de equilibrio para la tasa de pago y el empleo.

Digamos que el modelo de ecuaciones simultáneas para este escenario se compone de las siguientes dos ecuaciones**:

1. Demanda: n _t = β ₁ + β ₂ g _t + β ₃ p _t + ε _1t
2. Oferta: n _t = β ₁₁ + β ₁₂ m _t + β ₁₃ p _t + ε _2t

donde :

• n = número de enfermeras empleadas,
• p = tasa de ganancias,
• g = matriculación en la escuela de posgrado en enfermería,
• m = ingresos medios de las enfermeras empleadas.

**Estas fórmulas son solo ecuaciones de regresión diseñadas para este modelo específico; β es el coeficiente de regresión y ε es el término de error : factores inesperados que pueden colarse en el modelo.

Uso del modelo para resolver problemas

¿Recuerdas esas ecuaciones simultáneas del álgebra? Se pueden resolver juntos para encontrar valores para x e y. De la misma manera, las ecuaciones en SEM también se pueden resolver. Utilizando el ejemplo anterior, supongamos que desea averiguar el impacto parcial del salario medio (m) tanto en el número de enfermeras empleadas (n) como en la tasa de pago (p). Puedes modelar esto resolviendo las ecuaciones para n y p:

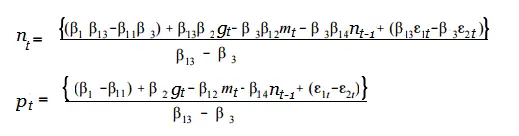
Modelos completos y modelos de ecuaciones estructurales

Cuando el número total de variables endógenas es igual al número de ecuaciones, se denomina SEM completo . Las variables endógenas son similares (pero no exactamente iguales) a las variables dependientes ; Tienen valores que están determinados por otras variables en el sistema (estas «otras» variables se llaman variables exógenas ). Si la tasa de ingresos y el número de enfermeras empleadas son las únicas dos variables endógenas en el ejemplo anterior, entonces este SEM está completo. Un SEM completo se denomina modelo de ecuaciones estructurales .

Modelado de ecuaciones estructurales y relación con modelos de ecuaciones simultáneas

Los términos modelado de ecuaciones estructurales y modelado de ecuaciones simultáneas son similares, y a menudo se confunden, pero no son exactamente lo mismo. La base de cualquier técnica de modelado estadístico es un conjunto de ecuaciones simultáneas. Los modelos de ecuaciones estructurales utilizan estas ecuaciones y son modelos completos de ecuaciones simultáneas. “Completo” significa que el número total de variables endógenas es igual al número de ecuaciones del modelo. En otras palabras, si el número de variables endógenas en su modelo no es igual al número de ecuaciones, entonces no es un modelo de ecuaciones estructurales.

Las variables principales utilizadas en el Modelado de ecuaciones estructurales suelen ser variables latentes , que se comparan con las variables observadas en el modelo. Una variable latente u “oculta” no es directamente medible u observable. Por ejemplo, el nivel de neurosis, escrupulosidad o apertura de una persona son variables latentes. Las variables latentes están siempre presentes en casi todos los análisis de regresión, porque todos los términos de error aditivos no son medibles (y, por lo tanto, son latentes).

En algunos casos específicos, se utiliza el modelado de ecuaciones estructurales para crear un modelo; Una de las técnicas de modelado más comunes, el análisis de regresión , es un caso especial de modelado de ecuaciones estructurales.

Tres técnicas de modelado

El análisis factorial es un tipo de SEM.

Modelado de ecuaciones estructurales es un término general para un conjunto de tres técnicas de modelado en estadística. Suele utilizarse para confirmar que un modelo elegido es válido. En otras palabras, se usa para probar si un modelo representa con precisión los datos de muestra . A diferencia de la mayor parte de las técnicas estadísticas, el modelado de ecuaciones estructurales puede manejar relaciones teóricas complejas entre múltiples conjuntos de variables. Esta técnica también tiene en cuenta el error de medida , algo que las técnicas estadísticas básicas no hacen.

Los modelos de ecuaciones estructurales buscan relaciones entre conjuntos de variables latentes. Desarrollado por primera vez en la segunda mitad del siglo XX por Karl G. Jöreskog, combina el análisis de trayectoria y el análisis factorial confirmatorio. Las tres técnicas incluidas en el término genérico Modelado de ecuaciones estructurales son:

• El análisis de regresión sólo se ocupa de las variables observadas . En la regresión, se predice una variable dependiente utilizando un conjunto de variables independientes . Por ejemplo, el peso de un paciente se usa para predecir su riesgo de diabetes. La regresión es una de las primeras técnicas de modelado y fue posible después del desarrollo del coeficiente de correlación de Karl Pearson .
• El análisis de rutas , desarrollado por el biólogo Sewell Wright a principios del siglo XX, puede utilizar variables observadas o una combinación de variables observadas y latentes. Básicamente, un modelo de ruta es un análisis de regresión con variables latentes. Por ejemplo, es posible que desee predecir cómo las tasas de interés y el PNB influyen en el gasto y la confianza del consumidor.
• El análisis factorial busca relaciones entre conjuntos de variables latentes («factores»). Puede responder preguntas como «¿Mi encuesta de diez preguntas mide con precisión un factor específico?». Spearman (1904) fue la primera persona en utilizar el término análisis factorial; lo usó para encontrar una construcción de dos factores para la inteligencia. Posteriormente, se desarrolló el análisis factorial confirmatorio para probar si un conjunto de variables latentes representaba con precisión un constructo. El análisis de clases latentes es muy similar; la principal diferencia es que LCA incluye variables dependientes categóricas y Factor Analysis no.

Siguiente : Índice de ajuste

Referencias:
C. Spearman. “Inteligencia general”, determinada y medida objetivamente. El Diario Americano de Psicología. vol. 15, No. 2 (abril de 1904), págs. 201-292
Karl G. Jöreskog. Modelado de ecuaciones estructurales con variables ordinales. Apuntes de conferencias: serie de monografías. Volumen 24, 1994, 297-310.
Randall E. Schumacker, Richard G. Lomax. Una guía para principiantes sobre el modelado de ecuaciones estructurales: Cuarta edición